Class 23 (Resampling)
Resampling or Discrete-Time Sampling
Overview
In many situations in signal processing, controls, and communications, we may want to change the rate at which we had originally sampled a discrete-time signal. We refer to this process as resampling or discrete-time sampling. In this lecture, we talk about downsampling (also known as decimation), decreasing the sampling rate by an integer factor $N$, and upsampling (also known as interpolation), increasing the sampling rate by an integer factor $M$.
Downsampling
Downsampling by 2
The basic downsampling operation is downsampling by 2. Mathematically, downsampling a signal $x[n]$ by 2 is defined by $$x_d[n] = x[2n] \; .$$ Notice that this is essentially a ``time-shrinking'' of the discrete-time signal by removing every other value. In time, the difference between this operation in discrete-time and continuous-time though is that we must now throw away samples.
In frequency, the difference between this operation in discrete-time and continuous-time is a little more complicated. Rather than stretching across frequency by a factor of 2 and dividing by 2 (the result in continuous-time), we individually stretch and divide each period of the DTFT around the integers of $2 \pi$ and then sum the results.
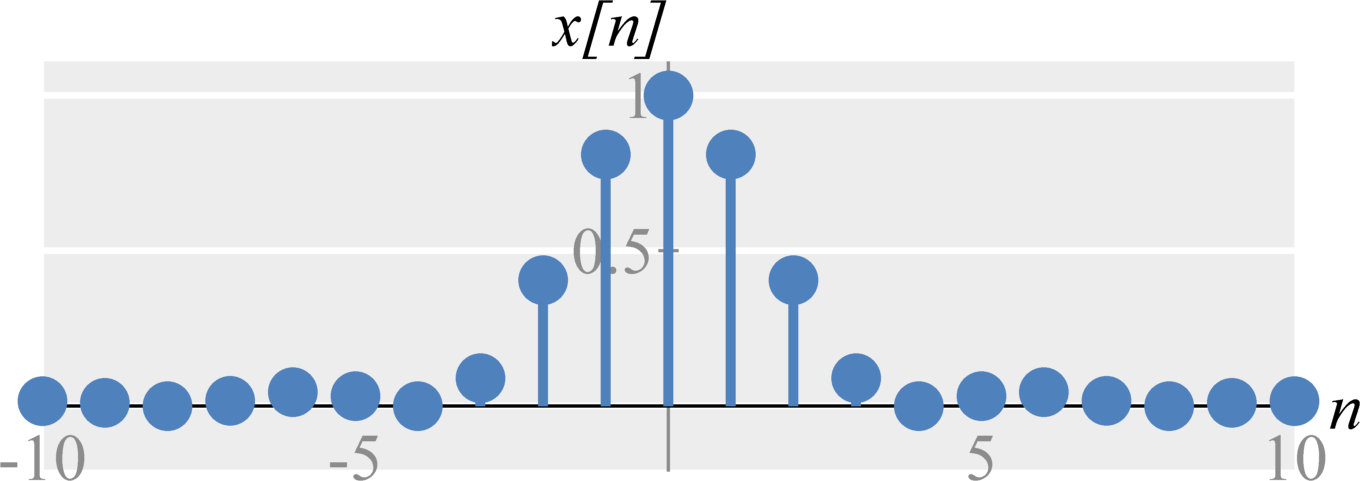
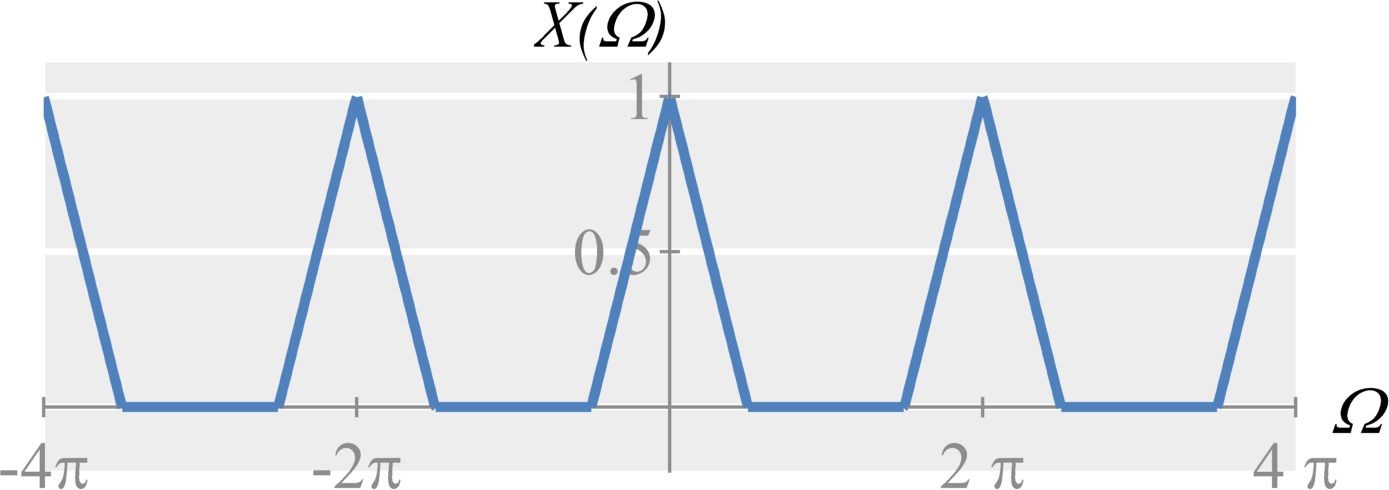
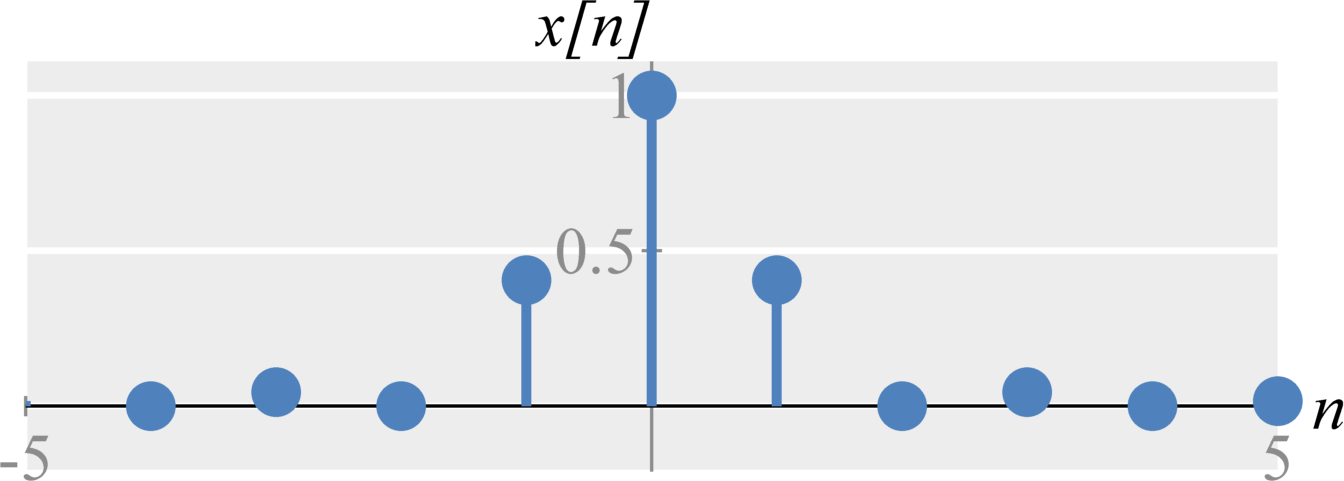
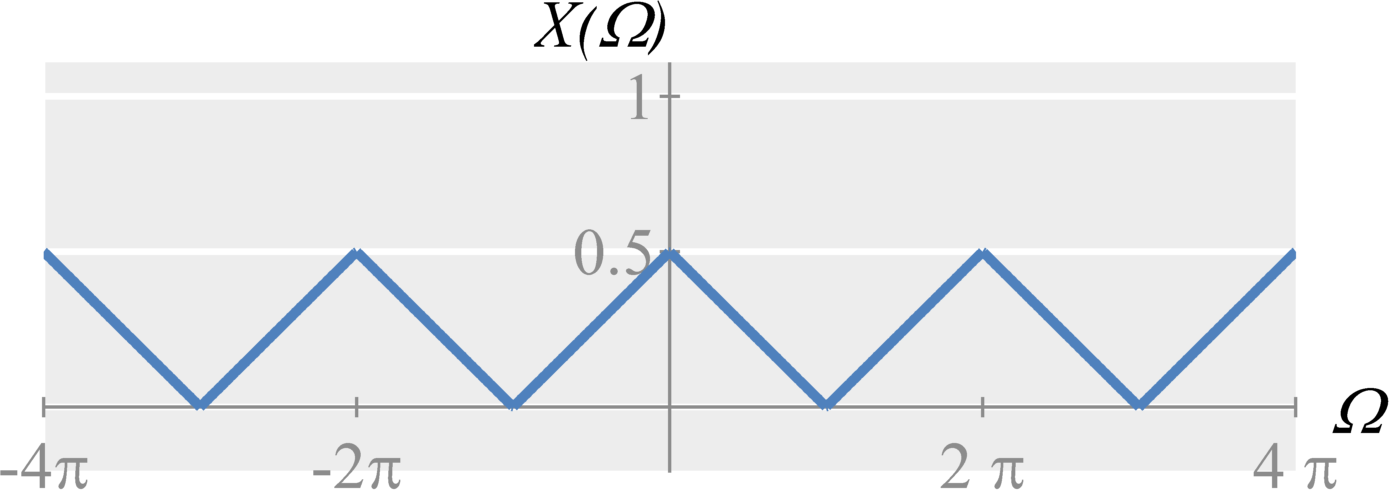
Downsampling by N
We can extend the concepts above to downsample by any integer number $N$. Downsampling a signal $x[n]$ by $N$ is defined by $$x_d[n] = x[Nn] \; .$$ That is, we keep only every $N$-th sample from $x[n]$. In frequency, we again see the same ``periodic stretching,'' except we now stretch by a factor of $N$ and divide the amplitude by $N$.
Aliasing from downsampling
As with continuous-time sampling, we can experience aliasing from downsampling (discrete-time sampling). Graphically, if the frequency content is stretched too much, we will get overlap (aliasing) and will no longer be able to perfectly reconstruct the original signal. If the maximum frequency stretches beyond $\Omega = \pi$, we get aliasing.
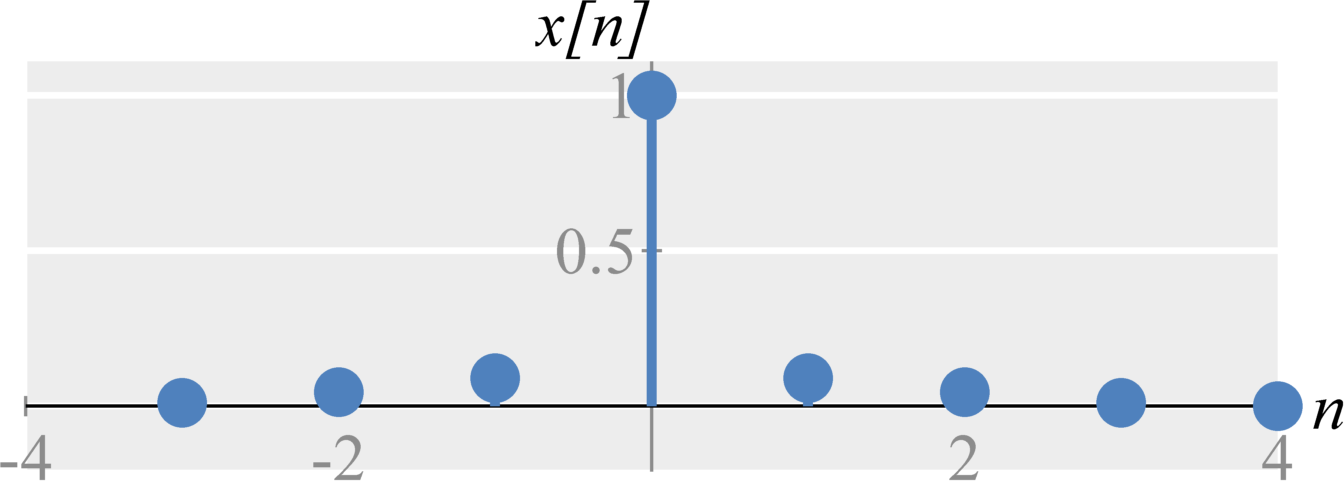
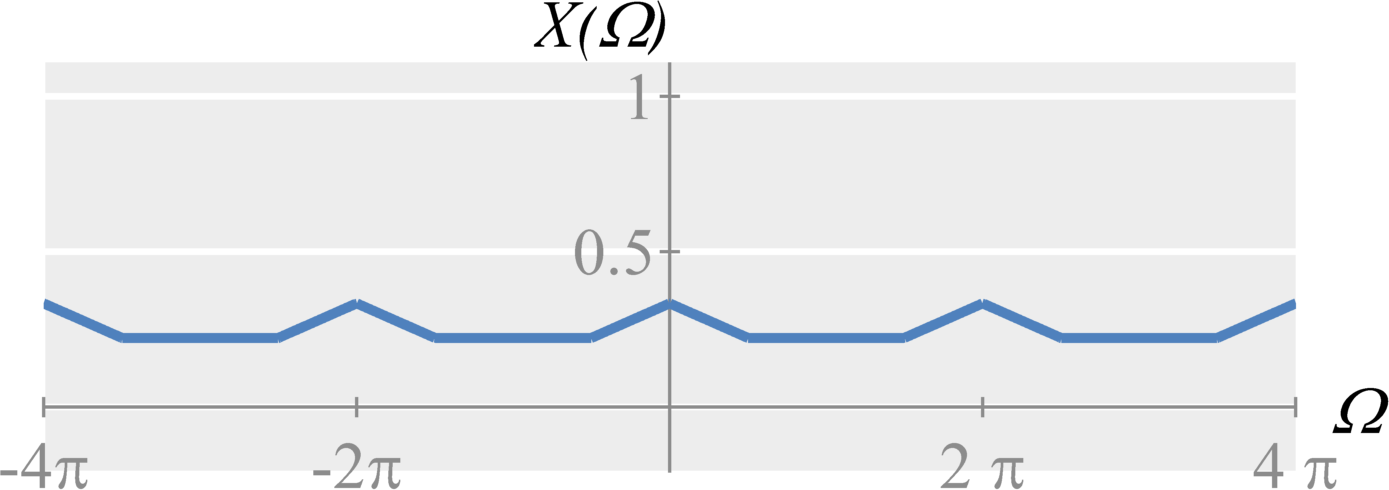
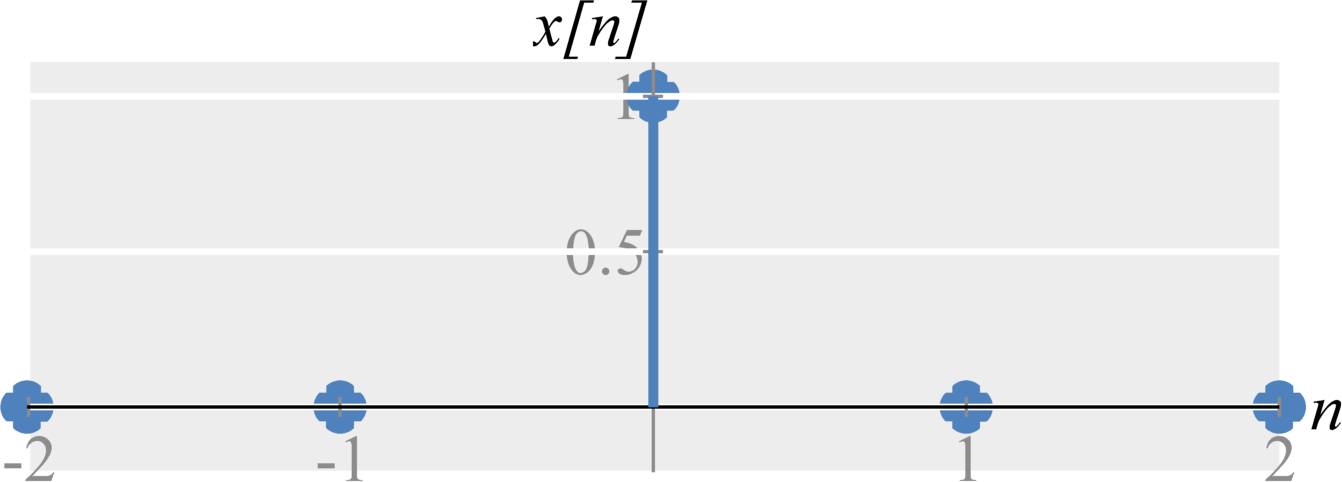
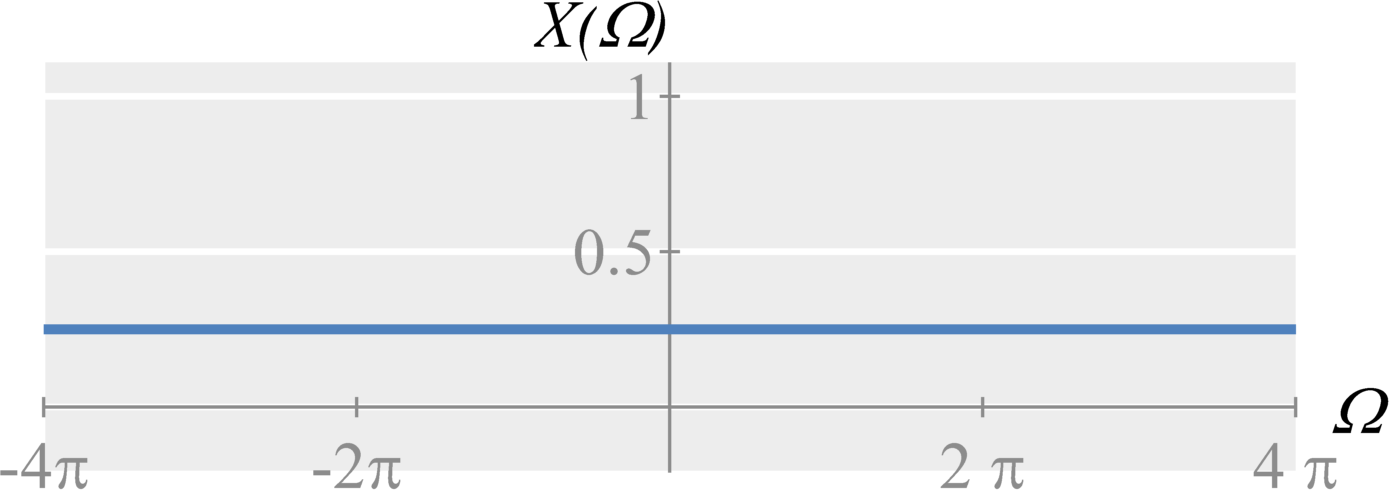
Anti-Aliasing
To counter aliasing, signals filtered using a low-pass, discrete-time anti-aliasing filter before downsampling. To ensure that aliasing does not occur, the cut-off frequency of an ideal filter would ideally be $\Omega_c = \pi/N$, where $N$ is the downsampling factor, and the gain would be $1$.
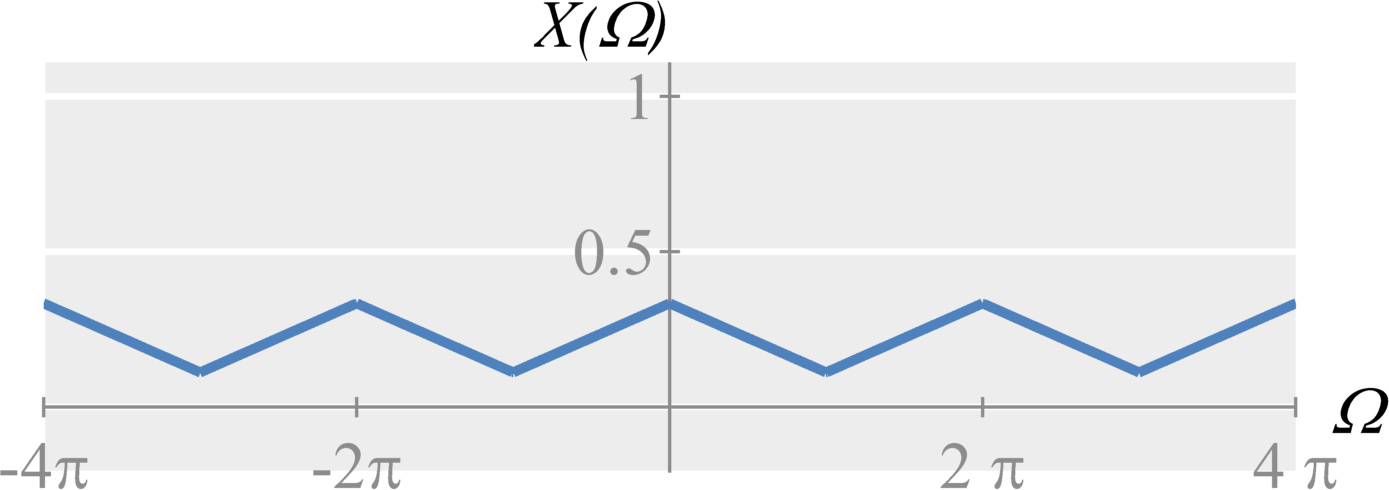
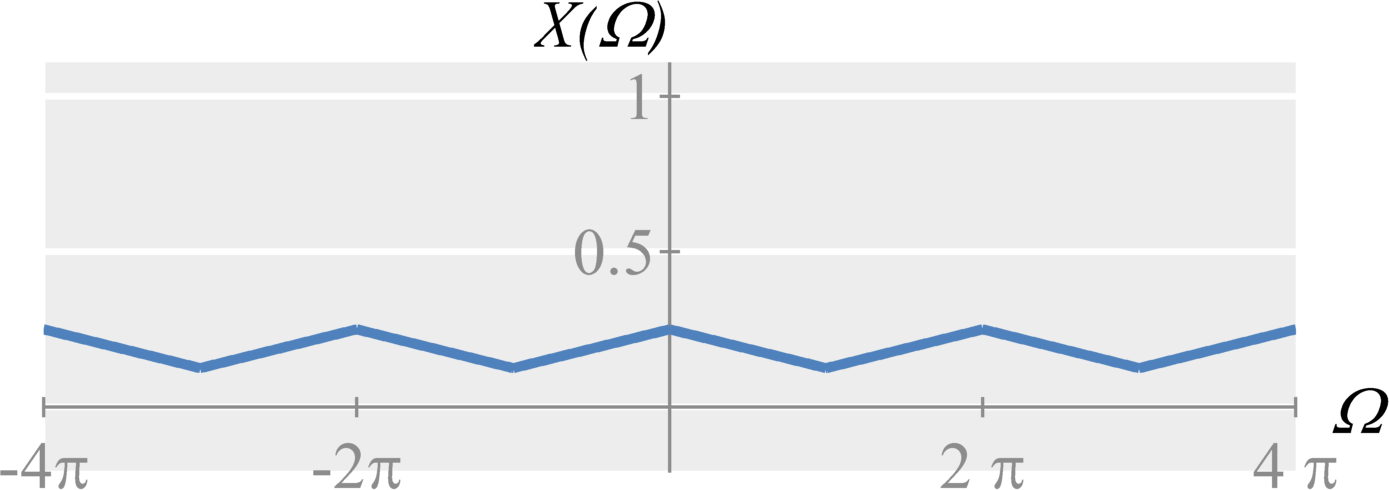
Upsampling
Upsampling by 2 (without interpolation)
The basic upsampling operation is upsampling by 2. Upsampling may refer to two similar operations: upsampling without interpolation or upsampling with interpolation (sometimes just called interpolation).
Mathematically, upsampling a signal $x[n]$ with DTFT $X(\Omega)$ by 2 without interpolation is defined by $$X_u(\Omega) = X(2 \Omega) \; .$$ Notice that this is essentially a frequency-shrinking of the DTFT signal. In the time-domain, this is equivalent to adding an extra zero between every sample.
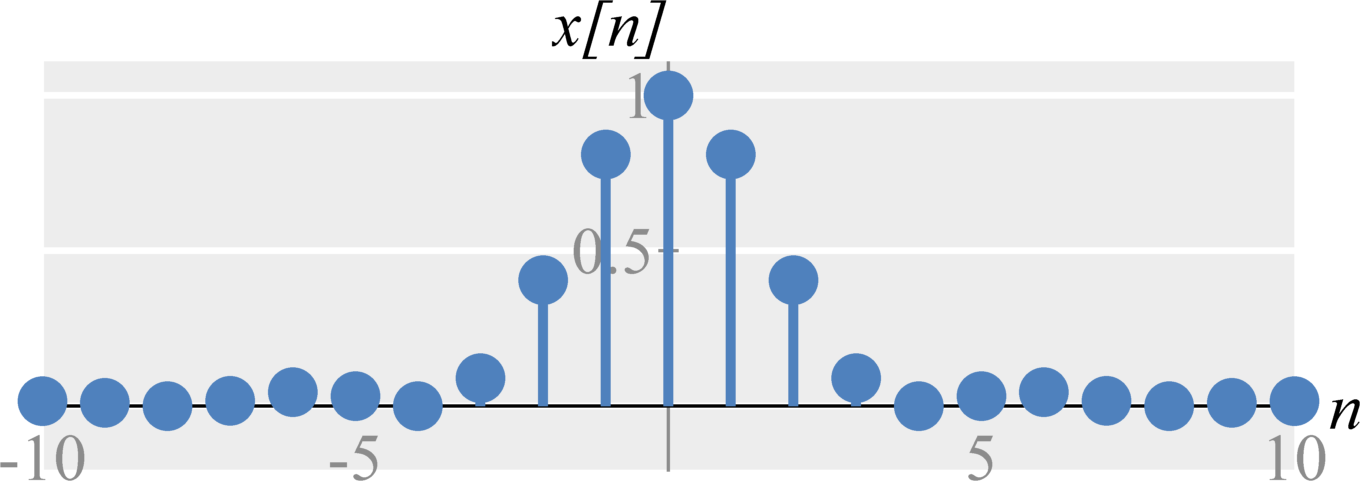
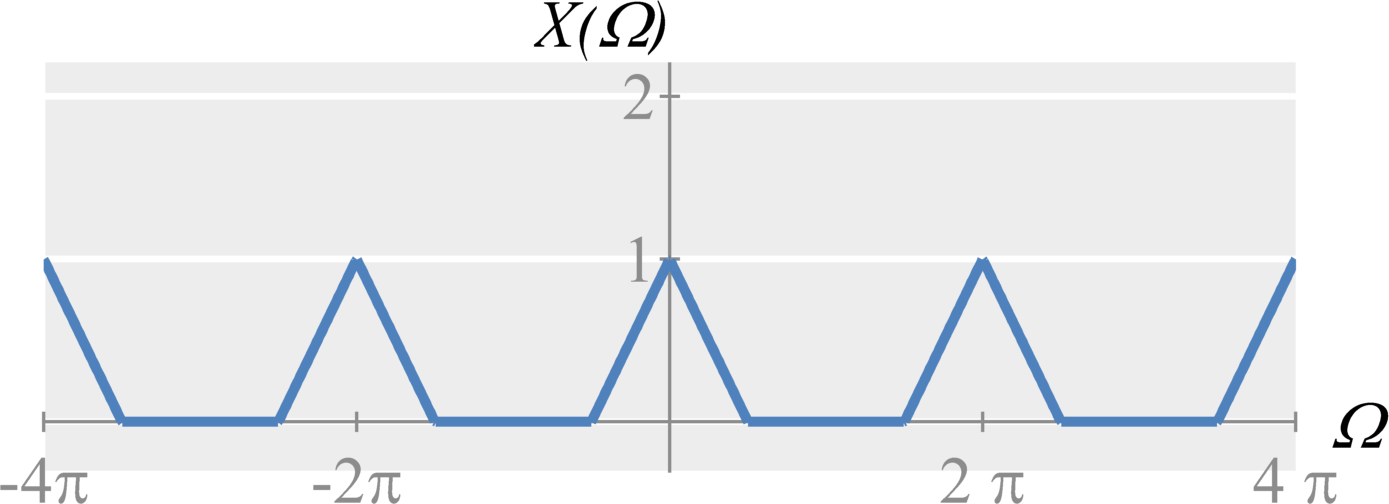
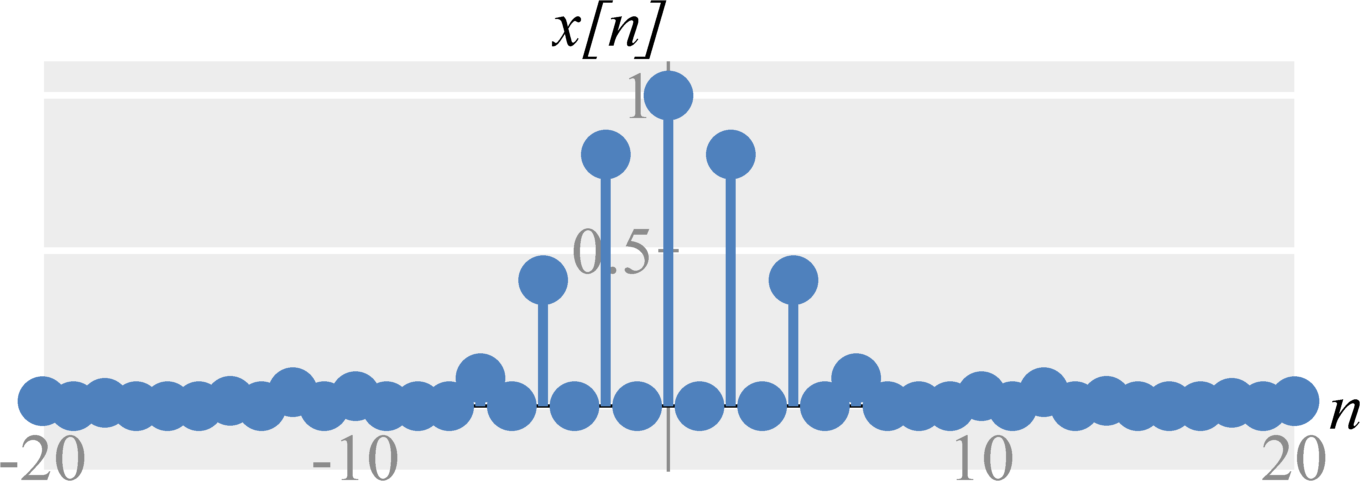
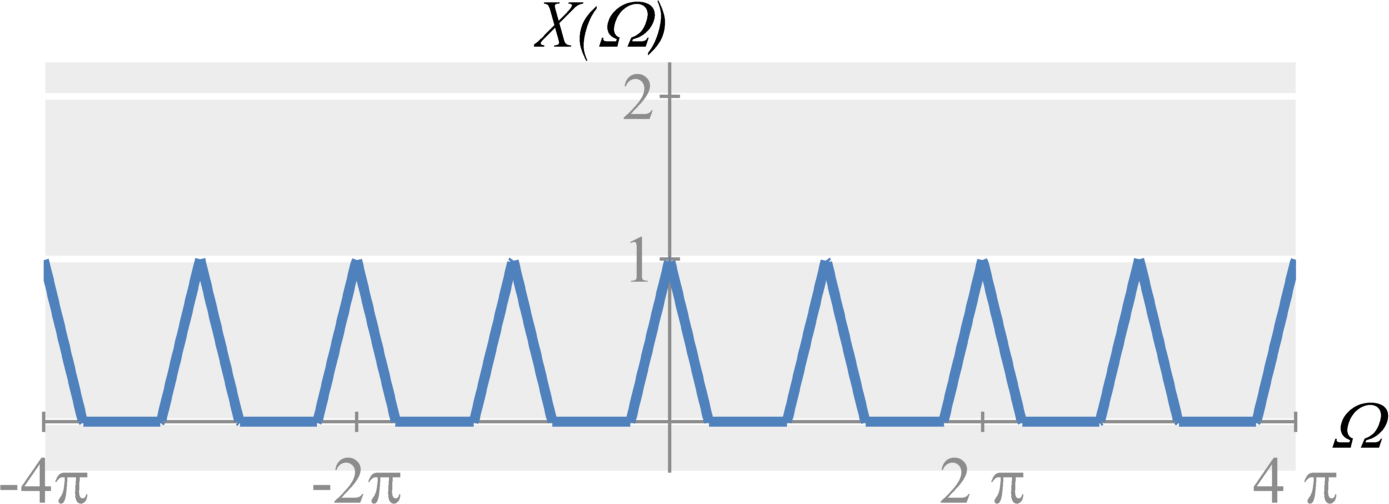
Upsampling by M
We can extend the concepts above to upsample by any integer number $M$. When upsampling a signal $x[n]$ by $M$, we add $M-1$ zeros between each sample. In frequency, this is defined by $$X_u(\Omega) = X(M \Omega) \; .$$ where we now shrink the frequency domain by a factor of $M$.


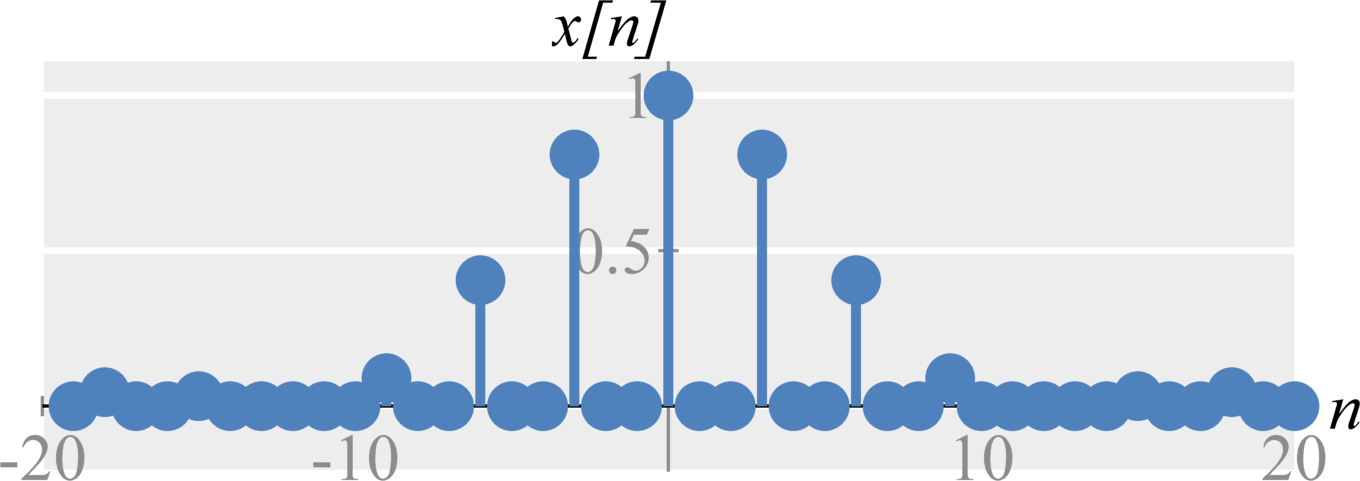
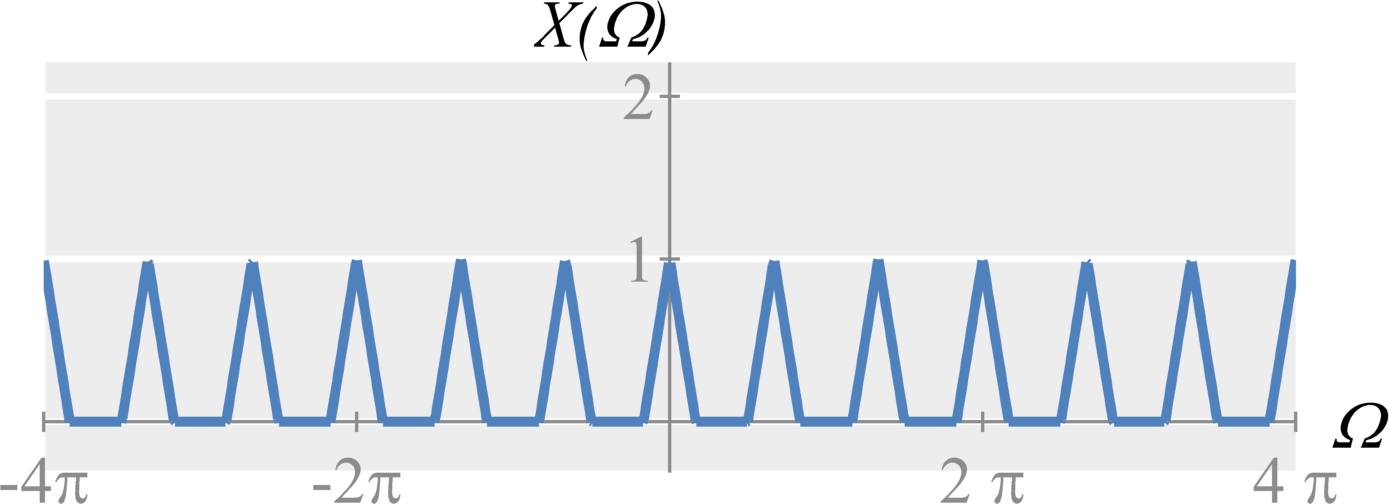
Upsampling by M (with interpolation)
Interpolation is equivalent to applying a low-pass filter to remove the high frequency replica's created by shrinking in frequency. In time, this removes all of the extra zeros and smooths the signal. To remove the high frequency components, the cut-off frequency of an ideal reconstruction/interpolation filter would ideally be $\Omega_c = \pi/M$, where $M$ is the downsampling factor and the gain would be $M$.




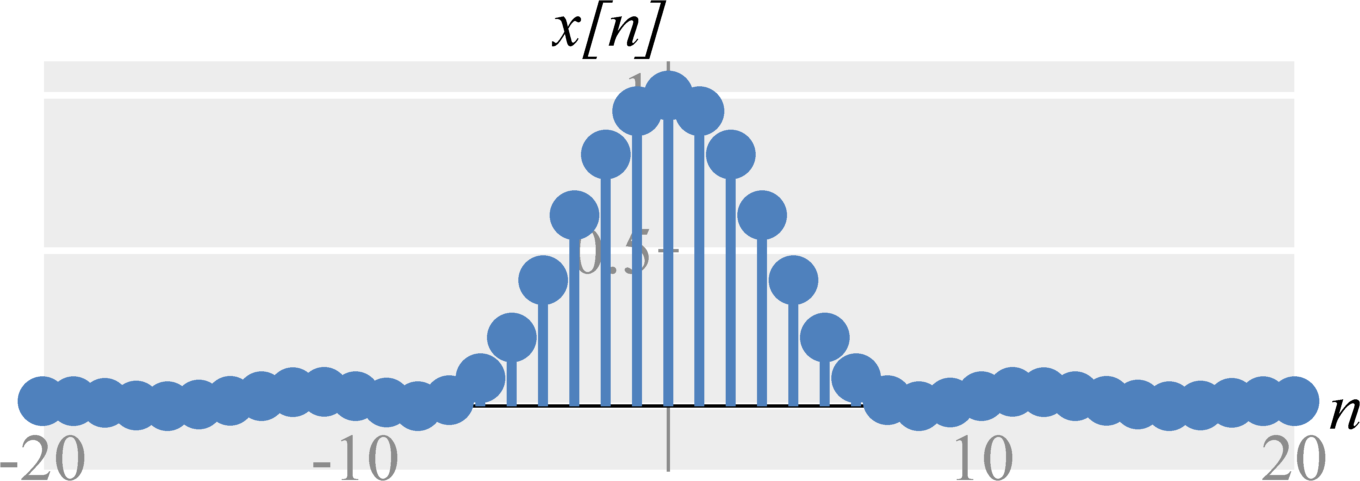
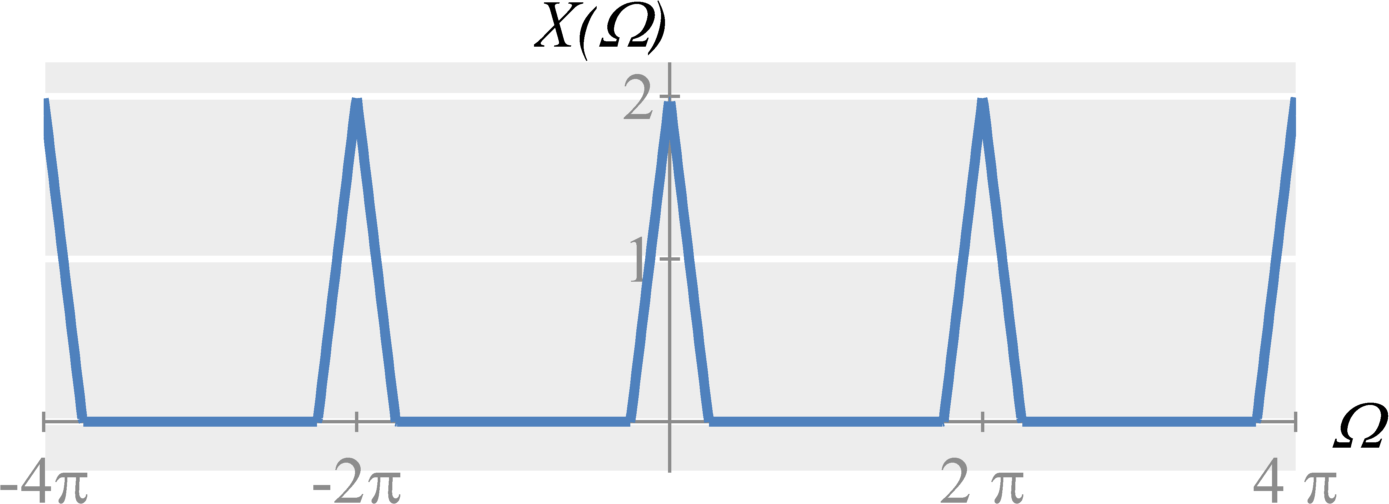
Additional Resources
- From this course
- Other online resources